Formule generali.
Il problema dei Marinai, delle Scimmiotte e delle Noci di cocco con le sue varianti può anche essere risolto velocemente, mediante l’uso di quattro formule generali, frutto di un altro mio studio molto impegnativo, con le quali è possibile calcolare direttamente i valori N e n, le Noci della primitiva raccolta e le Noci destinate ad ogni Marinaio dopo la spartizione finale.
In merito alle noci di ricompensa è opportuno sottolineare che il generico problema che presenta, ad esempio, tre Scimmiotte destinatarie di tre Noci di ricompensa per ognuna, in termini matematici è del tutto equivalente al problema con nove Scimmiotte e una sola Noce di ricompensa. Per tale ragione d’ora in poi tratteremo solo problemi che prevedono un sola Noce di ricompensa per ogni Scimmiotta e le formule più avanti trascritte sono riferite ai problemi generali con un numero qualsiasi di Marinai, di Scimmiotte e con una sola Noce di ricompensa.
Le formule sono distinte per i valori pari e per i valori dispari del numero m dei Marinai. I primi termini di queste formule hanno cinque indici; N è l’indice del numero delle Noci iniziali; m è l’indice del numero dei Marinai; n è l’indice del numero delle Noci finali; s è l’indice del numero delle Scimmiotte; k è la serie dei numeri interi positivi maggiori di zero. D, P, valori Pari e valori Dispari di m. Nei secondi termini si trovano due parametri speciali, t.e e t.d, che più avanti saranno trattati in dettaglio.

Le formule.

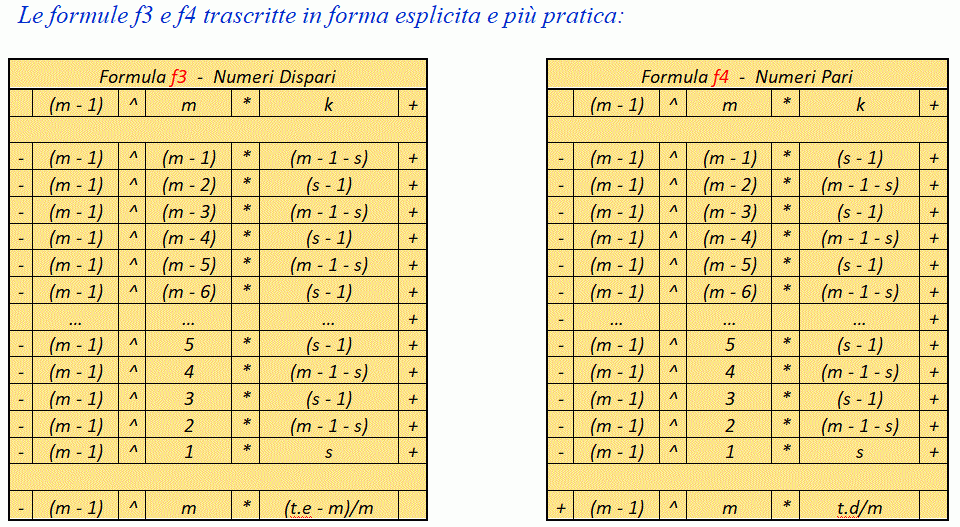

Le formule f1 e f2 che restituiscono il valore di N per m dispari e per m pari hanno tre addendi in ogni problema.
Le formule f3 e f4 che restituiscono il valore di n per m dispari e per m pari sono formate da un numero variabile di addendi, proporzionale al valore m e pari a (m + 1).
Ad esempio per m = 9 ed s =1, la formula f1 che restituisce il valore N ha tre addendi e la formula f3 che restituisce il valore n ha dieci addendi.

Parameti t.e t.d.
I due parametri t.e, t.d, in queste formule, sono numeri interi positivi da calcolare e dimensionare preventivamente mediante arrotondamento del valore s, per eccesso nel caso di t.e o per difetto nel caso di t.d. Questo valore s deve essere elaborato e reso multiplo del valore m. In merito è opportuno ricordare che per definizione ogni numero intero è multiplo di se stesso e che il numero zero è multiplo di ogni numero intero.
Parametro t.e.
Si trova nelle formule f1 e f3, relative ai valori dispari di m e richiede arrotondamento per eccesso.
Il valore s, come detto sopra, deve diventare multiplo di m; questo valore multiplo deve essere ricercato e individuato nella serie dei numeri maggiori di s il cui primo elemento utile per la ricerca è proprio il valore s.
Tra gli infiniti multipli presenti in questa serie il valore ricercato è il primo e il più vicino a s e può essere maggiore o uguale allo stesso valore s.
Parametro t.d.
Si trova nelle formule f2 e f4, relative ai valori pari di m e richiede arrotondamento per difetto.
Il valore s, come detto sopra, deve diventare multiplo di m; questo valore multiplo deve essere ricercato e individuato nella serie dei numeri minori di s il cui primo elemento utile per la ricerca è proprio il valore s e l’ultimo è il numero zero.
Tra i multipli disponibili in questa serie il valore ricercato è il primo e il più vicino a s e può essere minore o uguale allo stesso valore s.
Dalla regola generale deriva il caso particolare in cui m = s, con m pari o dispari. In questo caso i parametri t.e o t.d assumono lo stesso valore comune a m e ad s, ovvero, t.e = m = s ed anche t.d = m = s.
Proponiamo adesso due tabelle esemplificative relative a due serie di problemi con cinque e con quattro Marinai;

Parametro t.e – Numeri Dispari.
– Con cinque Marinai e una Scimmiotta, il valore di partenza è s = 1; questo numero deve essere arrotondato per eccesso perché diventi multiplo del valore 5 di m. Ora il primo valore multiplo di 5 disponibile al di sopra di 1 è proprio il valore 5 e in questo caso il parametro assume il valore t.e = 5.
– Con cinque Marinai e cinque Scimmiotte, il valore di partenza è s = 5; in questo caso il primo valore multiplo del valore 5 di m, uguale o maggiore di 5, è proprio il numero 5 stesso e il parametro assume il valore t.e = 5.
– Con cinque Marinai e sei Scimmiotte, il valore di partenza è s = 6; il parametro assume il valore t.e = 10, il multiplo di 5 più vicino al valore 6.
– Con cinque Marinai e sette Scimmiotte, il parametro mantiene lo stesso valore t.e = 10 che anche in questo caso è il multiplo di 5 più vicino al valore 6.
– Con cinque Marinai e undici Scimmiotte, il parametro assume il valore t.e = 15, il multiplo di 5 più vicino al valore 11.
– Con cinque Marinai senza Scimmiotte, il parametro assume il valore t.e = 0, il primo valore multiplo del valore 5 di m.
Parametro t.d – Numeri Pari.
– Con quattro Marinai e nove Scimmiotte, il valore di partenza è s = 9; il parametro in questa ipotesi acquisisce il valore t.d = 8, il primo dei multipli di 4 che si trovano al di sotto del valore 9.
– Con quattro Marinai e sette Scimmiotte, il parametro assume il valore t.d = 4, il primo dei multipli di 4 che si trovano al di sotto del valore 7.
– Con quattro Marinai e dodici Scimmiotte, il parametro assume il valore t.d = 12, il primo dei multipli di 4 disponibile nella serie s che partendo dallo stesso valore 12 si sviluppa nei suoi valori inferiori.
– Con quattro Marinai e una Scimmiotta, il parametro assume il valore t.d = 0, l’unico valore disponibile nella serie.
– Con quattro Marinai e nessuna Scimmiotta, il parametro assume il valore t.d = 0, l’unico valore disponibile.

Alcuni esempi di applicazione delle formule.
Formula f1

Formula f2

Formula f3

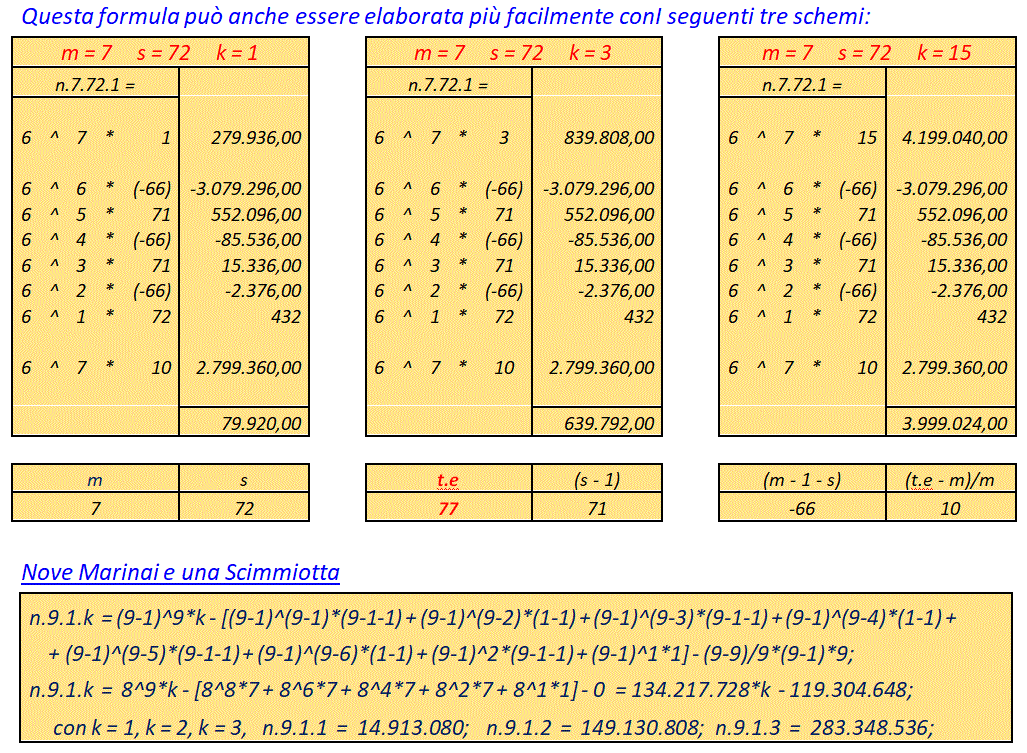
Formula f4

Per concludere.
Il metodo risolutivo sopra trattato, come già ricordato, può essere esteso a qualsiasi problema, con qualsiasi numero di Marinai, di Scimmiotte o di ricompense e si può quindi realizzare una vera e propria generalizzazione del problema.
Limiti.
Esistono due limiti, legati al numero m dei Marinai e al numero s delle Scimmiotte. Per il numero m dei Marinai il limite è d’ordine pratico. I problemi che hanno un numero di Marinai uguale o superiore a tredici unità danno luogo a numeri molto grandi il cui calcolo e la cui gestione presentano difficoltà via via sempre più rilevanti che nulla aggiungono o tolgono alla bellezza del problema. Personalmente preferisco evitare problemi di simile fattura, anche perché per altri versi non sempre è facile reperire calcolatrici idonee all’impresa.
Per il numero s delle Scimmiotte è da notare che al crescere di s i due valori N e n tendono lentamente a diminuire con andamento oscillante, sino a quando, raggiunto un certo limite di s, il numero n assume valori negativi. Questo limite si raggiunge per s = (m – 1)^(m – 1).
Al crescere ulteriore di s anche il numero N comincia a restituire valori negativi e per certi valori di s ulteriormente elevati i problemi proposti non ammettono soluzioni. Aumentando il valore k questi problemi cominciano a restituire valori positivi e i problemi ammettono soluzioni. Una verifica, più che necessaria, può togliere qualsiasi dubbio.
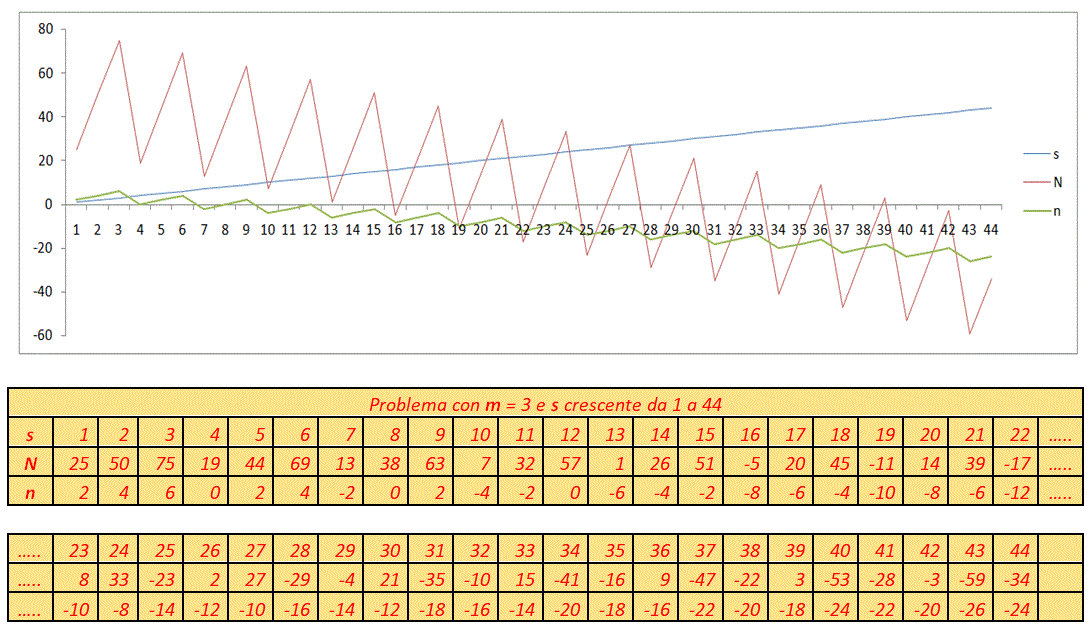
Il grafico che segue mostra la variazione di N e di n al crescere di s in un problema con tre Marinai. In questo caso il limite imposto dalla formula per il quale n = 0 è s = (3 – 1)^(3 – 1) = 2^2 = 4, e per tale valore il problema non ha soluzione. Al crescere di s, n e N presentano valori sempre più vicini al valore zero, sino a quando al valore particolare s = 40, n e N assumono definitivamente valori negativi.
Problemi con due Marinai

Il problema con due soli Marinai e una sola Scimmiotta, che ha il suo limite s = (2 – 1)^(2 – 1) = 1, non ha soluzione per k = 1. Per rintracciare una soluzione accettabile è necessario dare al numero k un valore maggiore.
Questo problema infatti restituisce N = 8k – 5, che per k = 1 assume il valore N = 3 non accettabile, perché a fine vicenda non rimangono Noci per la spartizione finale. Per k = 2, N assume il valore 11, accettabile perché a fine vicenda i due Marinai si ritrovano due noci per la spartizione finale e ad ognuno spetta una sola Noce. Vedi tabelline.
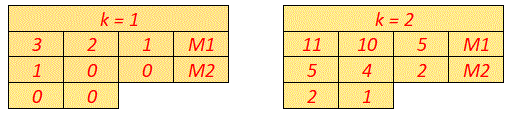
Tutti i problemi che presentano due soli Marinai e un numero di Scimmiotte maggiore di uno, per k = 1 non hanno soluzioni. Per rintracciare la prima soluzione utile di questi problemi è necessario utilizzare un valore k che a volte può anche essere elevato.
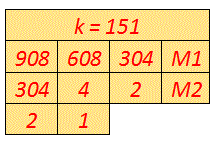
Per esempio, con m = 2 e s = 300, problema esclusivamente teorico, il primo valore di k che determina una soluzione accettabile deve essere addirittura pari a 151; in questo caso, N vale 908 ed a fine vicenda i due Marinai ricevono una sola Noce a testa nella spartizione finale.
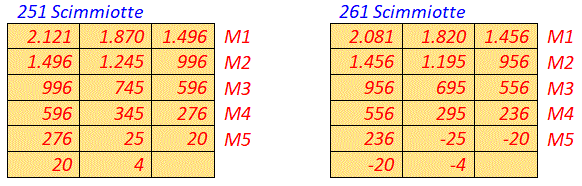
Il problema con 5 Marinai e 251 Scimmiotte, ove N.5.251.k = 15.625k – 13.504 ed N1 = 2.121, è valido, perché le Noci della spartizione finale sono 4. Il problema che vede 5 Marinai e 261 Scimmiotte, ove N.5.261.k = 15.625k – 13.544 ed N1 = 2.081, non è valido, perché restituisce nella sua tabella quattro valori negativi ed n assume il valore -4, condizione ovviamente inaccettabile e questo particolare problema, parimenti, non ammette alcuna soluzione. Vedi le tabelline.
A conclusione degli argomenti svolti ho inserito nella 3^ parte di questa trattazione alcuni problemi già svolti, arricchiti da formule, indicazioni e tabelle.


















