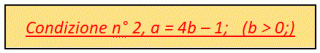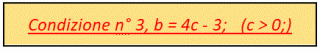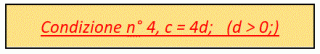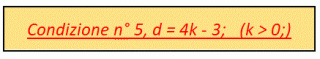2^ parte. Il metodo.
Nella versione classica appena descritta che, ripeto, prevede cinque Marinai e una sola Scimmiotta, destinataria peraltro del regalo di una sola Noce d’eccedenza a ogni passaggio, il problema è notoriamente governato dalla seguente equazione:

le due incognite variabili N, n, nell’ordine, sono i numeri – rigorosamente e ovviamente interi – delle Noci della primitiva raccolta e delle Noci assegnate a ogni Marinaio dopo la spartizione finale.
Questa formula è il risultato di una costruzione algebrica progressiva, svolta via via che si procede all’elaborazione delle condizioni imposte dal problema. Vediamo come.
Utilizzando un percorso a ritroso, consideriamo come punto di partenza delle nostre indagini il valore n della spartizione finale, che intuitivamente è anche il più piccolo dei numeri in gioco. Sappiamo che il valore precedente di n è cinque volte maggiore e lo indichiamo con 5n. Il valore ancora precedente, ricavato da un semplice ragionamento, è (5n * 5/4), espressione che per il momento lasciamo inalterata.
Procedendo a ritroso, abbiamo l’espressione (5n * 5/4 + 1) che è preceduta da (5n * 5/4 + 1) * 5/4, da (5n * 5/4 + 1) * 5/4 + 1 e da ((5n * 5/4 + 1) * 5/4 + 1) *5/4, e così via, in una sorta di “crescendo rossiniano” riepilogato nello schema che segue:

Come si può osservare, a ogni passaggio l’espressione si evolve e acquista sempre più volume, sino a quando alla cella 12 raggiunge la sua massima espressione, ovvero il valore di partenza N delle Noci della primitiva raccolta,

Tale unica formula, che pone in gioco due incognite e un denominatore, richiede per la sua risoluzione l’intervento delle Equazioni di Diofanto o delle Frazioni continue, procedimenti piuttosto complessi, di cui faremo a meno, perché seguiremo una diversa strategia basata sull’Algebra elementare.
Il procedimento che ho ideato e che sto per trattare interviene e si applica durante la costruzione sopra citata e consiste nella trasformazione e nella semplificazione della prima equazione della serie, la formula 5n * 5/4 della cella 3, che contiene il denominatore 4, con l’obiettivo preciso di “demolire” questo denominatore, in questo frangente e tutte le volte che si ripresenterà nelle formule successive dello schema.
La conseguenza immediata di questa elaborazione è che tutte le formule che si trovano a valle della formula semplificata subiscono una trasformazione consequenziale, la quale lascia – e deve lasciare – inalterati i risultati intermedi e i risultati finali. Non deve essere diversamente!
Scendiamo subito nei dettagli del metodo.
Nella cella 3 del nostro schema diamo corso al primo intervento; imponiamo e operiamo la 
nella quale il parametro a che vi figura, oggetto di future elaborazioni, è al pari di n, un numero intero positivo. La cella 3 diventa 25a, priva di denominatore; le successive celle, dalla cella 4 all’ultima del nostro schema, si trasformano e la cella 5 in particolare diventa (25a + 1) * 5/4.
Questa espressione ci ripresenta per la seconda volta un altro denominatore 4; ci proponiamo di eliderlo seguendo una strategia simile, ma un po’ più complessa. A tale scopo, consideriamo attentamente il parametro variabile a di questa formula. Se tale parametro assume, a titolo d’esempio, il valore 3, il binomio (25a + 1) diventa 76, multiplo di 4 e in grado di semplificarsi con il denominatore 4 citato, restituendo 19. Questo numero, subito dopo, moltiplicato per l’”innocuo” numeratore 5, restituisce il valore finale 95. Questa strategia continua a essere valida se oltre al citato numero 3 utilizziamo in alternativa i numeri 7, 11, 15, 19, 23, …, e tutti gli altri valori che fanno parte della serie a = 4b – 1, che un semplice studio ci permette di porre in opportuna evidenza. Adesso imponiamo e operiamo questa
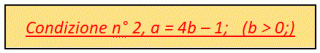
l’espressione della stessa cella 5 si trasforma e diventa quindi 125b – 30 e tutte le successive espressioni subiscono un nuovo cambiamento. Al passo successivo, quando il problema ci presenterà la nuova espressione (125b – 29) * 5/4, ci sarà sufficiente sostituire a b il valore 1 oppure gli altri suoi simili, 5, 9, 13, 17, 21,…, della serie b = 4c – 3; Imponendo quindi questa
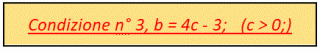
otteniamo il nuovo risultato 625c – 505 privo di denominatori. Procedendo in maniera analoga, al passo successivo troveremo l’espressione (625c – 504) * 5/4; porremo quindi la
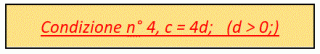
ed otterremo la nuova espressione 3.125d – 630 alla quale seguirà l’ultima espressione (3.125d – 629) * 5/4. In maniera analoga porremo infine l’ultima
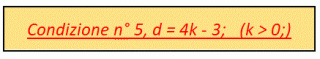
che ci restituirà l’espressione finale 15.625k – 12.504.
Tirando le somme, a fine lavoro, dopo avere imposto complessivamente cinque condizioni, otterremo la nuova equazione finale

lineare e priva di denominatori, con la quale possiamo calcolare agevolmente tutti i valori di N, le Noci della raccolta primitiva, in funzione del valore k da noi scelto a piacimento nella serie dei numeri interi positivi. A fine percorso avremo imposto in tutto cinque Condizioni,


queste, elaborate e sintetizzate, ci restituiranno la formula finale

che in maniera analoga ci restituirà tutti i valori di n, le Noci della spartizione finale, in funzione di k, la stessa serie dei numeri interi positivi.
 Riepiloghiamo.
Riepiloghiamo.
Il metodo applicato alla versione classica del problema ci ha fornito due formule finali, qui nuovamente trascritte


Ricordiamo che N nella prima formula è il numero delle Noci della primitiva raccolta mentre n nella seconda formula è il numero delle Noci che ogni marinaio riceve nella spartizione finale del bottino; questi numeri possono assumere infiniti valori in funzione della variabile k il cui minimo valore è k = 1. I primi valori di N e n ottenuti per k = 1, ovvero il risultato della versione classica del problema, sono i seguenti:
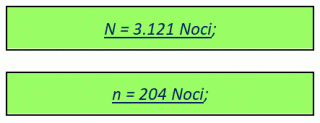
Applicando il metodo matematico sopra trattato si evince che il valore minimo matematico di Noci della raccolta primitiva perché l’intera vicenda possa avere luogo nelle modalità e nei termini descritti, deve essere paria a 3.121 Noci. Nella storiella si legge che i cinque Marinai, dopo questa raccolta primitiva si mettono a dormire. Ma si legge pure che non tutti dormiranno! Vediamo adesso cosa succede con tale quantitativo di Noci:
Un primo Marinaio M1, furtivamente e in ore notturne, si alza, raggiunge il bottino di Noci e lo suddivide in cinque parti di cui quattro sono formate da 624 Noci e una è formata da 625 Noci, con una Noce eccedente. M1 regala questa Noce eccedente alla Scimmiotta che gradisce molto l’omaggio, nasconde per se stesso un gruppo di 624 Noci ed ammucchia gli altri gruppi, che messi assieme formano un nuovo bottino, più modesto, di 2.496 Noci e quindi, sempre furtivamente, si rimette a dormire.
Un secondo Marinaio M2, subito dopo e sempre furtivamente raggiunge il luogo ove sono ammucchiate le Noci, suddivide questo nuovo bottino in cinque parti, di cui quattro formate da 499 Noci e una da 500 Noci; Regala la Noce eccedente alla felicissima Scimmiotta, nasconde per se stesso un gruppo di Noci ed ammucchia le altre, che formano un nuovo bottino di 1.996 Noci e se ne ritorna in silenzio a dormire.
Un terzo Marinaio M3, successivamente e in frangenti analoghi, suddivide il nuovo bottino in cinque gruppi, quattro formati da 399 Noci ed uno da 400 Noci; regala la Noce eccedente alla simpatica Scimmiotta, nasconde per sé un gruppo di Noci ed ammucchia le altre, che messe assieme ammontano a 1.596 Noci e quindi si rimette a dormire.
Un quarto Marinaio M4 in tempi successivi suddivide questo nuovo mucchio in cinque gruppi di Noci, quattro da 319 ed uno da 320; regala la Noce eccedente alla Scimmiotta, nasconde per sé un gruppo di Noci ed ammucchia le altre in un nuovo bottino, che ammonta a 1.276 Noci, dopodiché torna a dormire.
Il quinto Marinaio M5 ripete per ultimo le stesse vicende truffaldine, suddivide il bottino in cinque parti, quattro da 255 e una da 256 Noci, regala la Noce eccedente alla Scimmiotta, nasconde per sé un gruppo di Noci e raggruppa le altre che ammontano così a 1.020 esemplari e sempre di nascosto si rimette a dormire.
Il giorno dopo, al risveglio, i cinque Marinai con la coscienza sporca che chiude loro la bocca, suddividono il bottino rimasto in cinque parti che stavolta risultano tutte uguali e ognuno riceve alla fine 204 Noci. La Scimmiotta, convinta che anche qui avrebbe ricevuto una Noce di ricompensa, non riceve nulla e ci resta malissimo!
La versione classica del problema appena trattata, può essere arricchita da un secondo valore matematico, che si ottiene facilmente attribuendo alla variabile indipendente delle due formule generali il valore k = 2; con questo valore si ottengono N = 18.746 Noci della primitiva raccolta e n = 1.228 Noci che vanno ad ogni Marinaio dopo la spartizione finale.
Due note curiose e divertenti: Se i Marinai fossero solo due, sempre con una sola Scimmiotta, il numero di Noci della raccolta primitiva, nel rispetto delle regole matematiche imposte dal problema, dovrebbe essere pari a 3; ma questa soluzione non è accettabile perché con tale valore iniziale tutto il bottino basterebbe solo per dare una Noce di regalo alla Scimmiotta per ognuno dei due passaggi e per accontentare le bramosie truffaldine di un solo Marinaio, mentre l’altro Marinaio non avrebbe niente da rubare. Per ovviare a tale carenza è appena sufficiente attribuire alle due formule generali del problema il valore k = 2, per il quale si ottiene un valore iniziale N = 11 Noci; con questo valore iniziale a fine vicenda ognuno dei due Marinai riceve una sola Noce nella spartizione finale, dopo che nel corso della vicenda sono state garantite le due ruberie dei due protagonisti truffaldini e i due regali destinati alla Scimmiotta.
Se i Marinai fossero invece dieci e vi fosse sempre una sola Scimmiotta, la raccolta iniziale di Noci subirebbe un’impennata strabiliante; i dieci Marinai, sempre come minimo, dovrebbero raccogliere infatti un “pugno” di Noci ben più corposo, pari a 89.999.999.991 esemplari, quasi 90 miliardi di Noci. Ma … esiste un’isola deserta con tutta questa disponibilità di palme e Noci di cocco?